Growing AIVC = a priori knowledge + static architecture + dynamic states
Cells, the fundamental units of life, are crucial for understanding health, aging, and disease, and are essential tools in drug development and synthetic biology. However, cell-based experiments are resource intensive and prone to variability, contributing to the reproducibility concerns in biomedical research.
While the first carbon-based cell emerged through billions of years of evolution, the development of the first silicon-based cell now presents a transformative opportunity for the science community. The concept of virtual cell or digital cell, introduced circa 2000, initially relies on traditional low-throughput biochemical experiments to quantify spatiotemporal changes in substances involved in specific biological processes.1 These early models employed differential equations and stochastic simulations to model specific cellular processes. Pioneering whole-cell virtual models, such as those for Mycoplasma genitalium,2Escherichia coli3 and Saccharomyces cerevisiae,4,5 were primarily based on a priori knowledge. However, they lack rigorously designed matched perturbation omics data and spatiotemporal imaging data. While groundbreaking, these early models are limited in their ability to fully capture the dynamic nature and complexity of living cells, underscoring the need for more comprehensive data integration and advanced modeling approaches.
Recent advancements in high-throughput technologies and artificial intelligence (AI) have paved the way for more sophisticated virtual cell simulations. Bunne et al. 6 recently proposed the concept of Artificial Intelligence Virtual Cells (AIVCs), which integrate AI and multi-modal data to create comprehensive computational models of cellular functions. These AIVCs promise to enable precise and scalable in silico experimentation, potentially revolutionizing biomedical research by complementing or even replacing conventional experiments in certain scenarios, with high-throughput simulations.
Despite the promising outlook of AIVCs, several critical questions remain unanswered. Just as cell culture medium nourishes biological cells, what constitutes the ideal “culture medium” for growing these digital entities? Which cell types should we prioritize for virtual cultivation? Addressing these questions is crucial for realizing the full potential of AIVCs and their impact on drug development, disease modeling, and fundamental biological research. As we stand at the threshold of this new era in cellular modeling, the scientific community should collaborate to establish standards and best practices for AIVC development and validation.
Three data pillars for growing AIVCs
We propose here that the evolution or growth of AIVCs relies on three essential building blocks and nutrients: a priori knowledge, static architecture, and dynamic states. These data pillars, when combined with deep learning algorithms, form the foundation for AIVC development (Fig. 1).
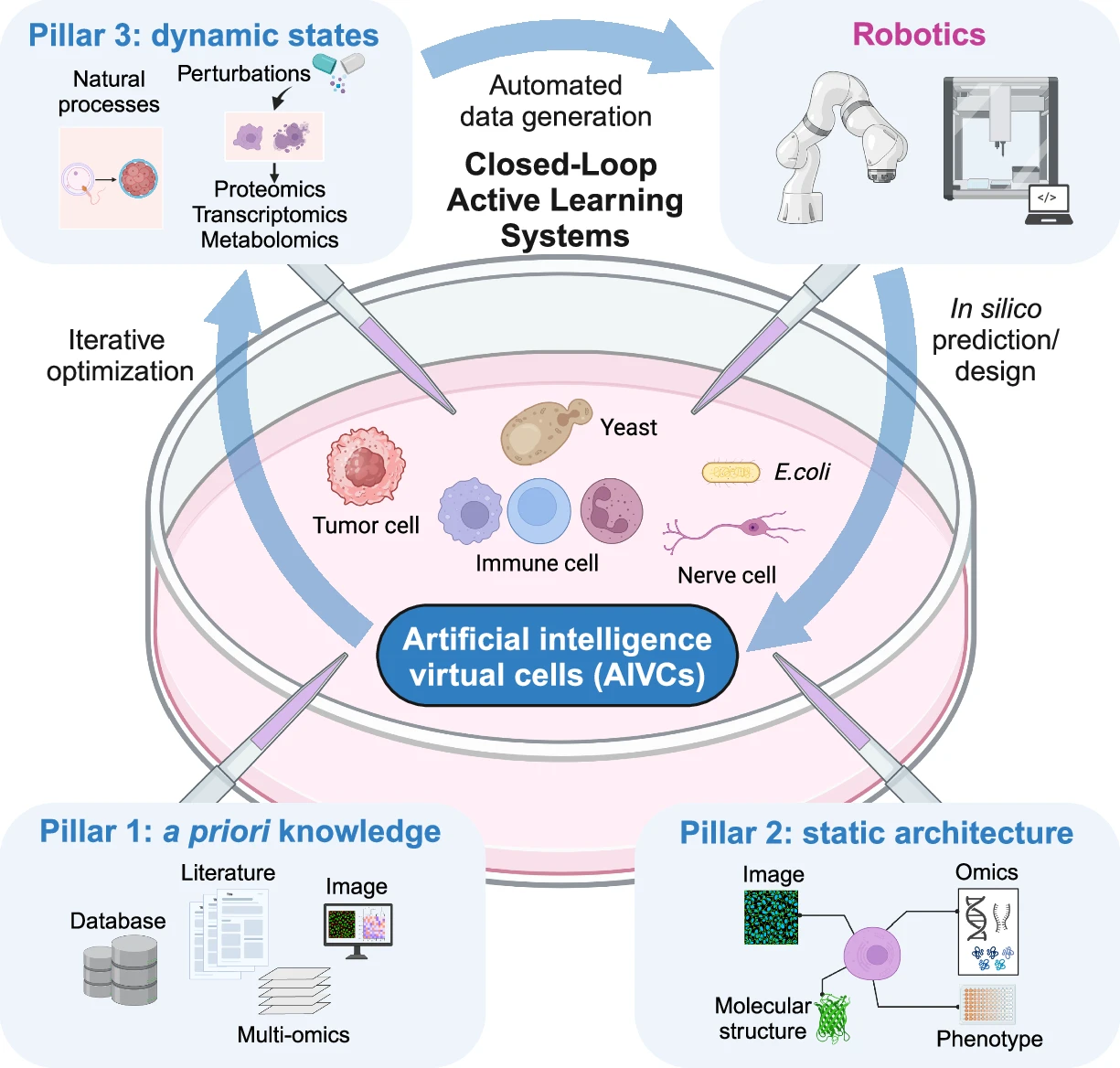
This schematic illustrates the three key pillars for growing AIVCs: a priori knowledge, static architecture, and dynamic states. These are integrated using AI algorithms to model cellular behavior, with examples of model organisms like E. coli, yeast and various cell lines. It also showcases the evolution of AIVCs using closed-loop active learning systems. In this advanced framework, computational predictions guide automated experimentation, with a particular focus on perturbation omics.
The biomedical community has generated vast amounts of cell-related data, including text-based literature, molecular expression data, and multi-scale imaging from the organismal to nanoscale level. With the rapid advancement of AI, we speculate that a comprehensive foundation model integrating all these data sources could be developed, serving as a fundamental basis for constructing AIVC. We designate a priori knowledge as the first pillar of AIVC construction. Despite its vast size and diversity, this knowledge base primarily consists of fragmented information across different cell types and populations. While it is unrealistic to build a fully functional AIVC for a specific cell type solely from these data, they encapsulate fundamental cell biological mechanisms essential for model construction. Furthermore, as these data already exist and require no additional generation cost for AIVC developers, they provide an ideal starting point for building AIVC.
However, while the a priori knowledge pillar is rich in diverse cell biology information, it cannot be directly used to construct a specific AIVC model. To achieve this, a comprehensive characterization of a specific cell is required, capturing its complete cellular structures at both the morphological and molecular expression levels, along with their interactions. We define this second essential pillar of AIVC construction as static architecture, which integrates nanoscale molecular structures and spatially resolved data from molecular modeling, cryo-electron microscopy, cryo-electron tomography, correlative light and electron microscopy, super-resolution fluorescence imaging, spatial omics, and other multi-scale analyses. Additionally, tissue expansion techniques7,8 can further enhance spatial resolution, complementing the high-resolution imaging methods and omics technologies mentioned above. This integrated approach provides a detailed three-dimensional context essential for accurate AIVC modeling.
While static data provide a bona fide snapshot of the cell, they fail to capture the dynamic nature of living systems. To construct a live AIVC, we introduce dynamic states as the third pillar for AIVC development. These data encompass natural processes such as aging, development, and carcinogenesis, as well as induced perturbations including physical, chemical, and genetic interventions. Cellular dynamics are historically studied by measuring the expression or activity of one or a few molecules at a time. With advancements in high-throughput omics technologies — such as transcriptomics, proteomics, and metabolomics — it is now possible to profile thousands of molecules across diverse cellular states. To build an effective AIVC, it is essential to comprehensively capture a wide range of cellular states and maximize their diversity to ensure high accuracy in differentiating them, requiring large volumes of dynamic, cell-specific data. Given the limited number of naturally occurring states, artificial perturbations serve as effective tools to generate different cellular states. Among these, perturbation proteomics is particularly valuable, as proteins are the primary structural components and catalysts of cellular biochemical processes.9 A recent AIVC pilot study integrating perturbation proteomics and AI algorithms demonstrates accurate prediction of drug efficacy and synergistic combinations, highlighting the critical role of dynamic perturbation proteomics data in constructing robust virtual cell models for drug discovery and cellular simulation.10
Although single-cell omics technologies have generated large datasets of millions of cells isolated from bulk tissues, their value for constructing AIVC is limited due to the similarity of the cells’ states. Antibody-based methods, such as those used in the Human Protein Atlas,11 are valuable, while mass spectrometry-based proteomics offers distinct advantages in analyzing thousands of proteins, protein post-translational modifications, and complex dynamics without the need for affinity-based reagents.12 To better understand the impact of perturbations on cellular behavior, emerging spatial omics technologies enable large-scale mapping of molecular distribution, providing insights into how perturbations alter cellular processes in their native spatial context. In particular, spatial proteomics represents the forefront of this advancement.8,13 In addition, innovative sample preparation methods now allow simultaneous multi-omics analysis of the same sample.14 We argue that the AI-driven integration of static and dynamic data is essential for constructing a functionally robust and predictive AIVC.
The integration of multimodal data from a priori knowledge, static architecture, and dynamic states demands sophisticated AI frameworks capable of hierarchical reasoning, cross-modal alignment, and predictive simulation. Foundational architectures such as transformers, convolutional neural networks, and diffusion models provide critical building blocks for data processing and feature extraction. Future advancements in AI algorithms will further enhance the fidelity, generalizability, and predictive power of AIVCs.
The ultimate purpose of these models is multifaceted, addressing key challenges in systems biology and personalized medicine. AIVCs aim to infer molecular states across omics layers, forecast molecular states based on physiological inputs, and predict cellular outcomes following perturbations or in specific conditions based on baseline molecular states. By integrating diverse data types and extracting complex, non-linear relationships across biological scales, AIVCs leverage their capacity to provide unprecedented insights into cellular behavior.
Evolution of AIVC: closed-loop active learning systems
To grow AIVCs, we foresee a transition from static, data-driven models to adaptive systems capable of evolving intelligence. While traditional approaches relied on passive data assimilation, modern closed-loop architectures will enable AIVCs to actively interrogate biological reality through AI model, autonomous robots, and dynamic data. The operational framework for closed-loop AIVC development draws inspiration from recent breakthroughs in autonomous chemistry laboratories.15 Central to this vision is the establishment of closed-loop frameworks that integrate computational prediction with robotic experimentation, specifically targeting gaps in dynamic state data (Fig. 1). Unlike static data repositories or fixed simulation parameters, closed-loop systems establish a self-optimizing workflow where AI algorithms continuously identify knowledge gaps in dynamic response patterns and automatically design and execute multiplexed perturbation experiments to resolve uncertainties in molecular interaction networks. The cycle is completed as the system validates predictions through real-time comparison of in silico and in vitro outcomes. This autonomous experimentation cycle fundamentally transforms the temporal resolution of model refinement. While classical approaches required years of manual hypothesis testing in exploratory synthetic chemistry research, closed-loop systems can gain equivalent knowledge through mere weeks of targeted robotic experimentation, dramatically accelerating the pace of scientific discovery and understanding.15
A critical challenge in modeling dynamic states is the combinatorial complexity of cellular responses to perturbations. While existing datasets capture snapshots of induced or natural states, they often lack systematic coverage of the parameter space. Our proposed closed-loop active learning systems could prioritize high-impact perturbations — such as CRISPR-based gene knockouts, small-molecule treatments, or optogenetic triggers — based on their potential to reduce model uncertainty or reveal novel regulatory mechanisms. For example, an AIVC trained on baseline proteomic profiles might identify understudied phosphorylation events in stress response pathways, prompting robotic platforms to perform time-resolved phosphoproteomics under targeted metabolic perturbations. This feedback loop will not only refine the model’s understanding of signaling dynamics but also generate purpose-built datasets that maximize biological insight per experiment. As robotic throughput increases and multimodal data integration matures, AIVCs may autonomously guide the resolution of longstanding questions in cell biology — from decoding context-specific protein functions to engineering synthetic cellular behaviors.
Low-hanging fruits
Selecting a proper cellular model for the inaugural AIVC is a crucial decision that will shape the development and validation of this groundbreaking technology. Several candidates merit consideration, each with its own advantages and limitations. As one of the simplest self-replicating organisms, mycoplasma offers a minimalist system for modeling. However, its unique biology may limit broader applicability. E. coli, the well-studied prokaryote, provides a wealth of existing data and a simple cellular structure. Its rapid growth and ease of genetic manipulation are advantageous, but it lacks the complexity of eukaryotic cells. As a eukaryote with subcellular organelles similar to human cells, yeast offers a balance between simplicity and relevance to higher organisms. Its genetic tractability and established role in biotechnology make it an attractive candidate. The immortalized human cancer cell lines (e.g., HeLa, HEK293) are widely used in research and associated with vast amounts of phenotypic and omics data.
While extensive experimental data exist for these cell types, significant gaps remain across the three pillars, particularly in their dynamic states. Notably, perturbation proteomics data, which are essential for building a comprehensive and dynamic AIVC, are scarce across all the candidate cell types.
We propose starting with a relatively simple yet informative model, such as S. cerevisiae. This organism has relatively small genomes and boasts a wealth of perturbation omics and imaging data, coupled with established protocols for genetic manipulation and high-throughput experiments. As a eukaryote, yeast presents a multi-compartmented cellular structure, providing an excellent platform to model complex intracellular organization and dynamics. This feature allows for a more comprehensive representation of eukaryotic cellular processes, bridging the gap between prokaryotic and higher eukaryotic systems. Moreover, the advantage of S. cerevisiae extends beyond basic research to applied fields such as synthetic biology and drug screening, enhancing the potential impact of the AIVC.
Although S. cerevisiae presents compelling advantages as an initial model, human cancer cell lines remain pivotal candidates for subsequent AIVC development. Their pervasive use in biomedical research, immediate relevance to human pathophysiology, and potential to revolutionize drug discovery and personalized medicine render them invaluable targets for AIVC modeling.
Developing an AIVC for these simpler organisms can serve as a proof of concept, allowing us to address fundamental questions posed by Bunne et al.6: What are the specific data needs and requirements for building an AIVC? How much data is necessary to construct a robust and predictive AIVC? How can we develop a comprehensive and adaptable benchmarking framework to evaluate AIVC performance? By tackling these questions with a simpler model organism, we can refine our methodologies and establish best practices before advancing to more complex cellular systems. This stepwise approach will provide valuable insights into the scalability of the AIVC concept and inform future efforts to model more complex eukaryotic cells and cell populations.
Conclusion and outlook
As we create and grow AIVCs in the digital petri dish of modern biomedical research, we must carefully consider the “nutrients” that will nourish their growth. Our proposed three data pillars of a priori knowledge, static architecture, and dynamic states form the essential medium for these in silico entities. Among these, perturbation-based omics data — transcriptomics, proteomics, and metabolomics — emerge as the critical growth factors.
To efficiently generate this wealth of perturbation data, we envision Closed-Loop Active Learning Systems as the next evolutionary step. These systems, inspired by autonomous chemistry laboratories,15 will seamlessly integrate AI-driven predictions with robotic experimentation. Like a skilled gardener, they will identify knowledge gaps, design targeted experiments, and continuously refine our understanding of cellular complexities. The journey from static models to adaptive, self-optimizing AIVCs promises to revolutionize drug discovery, disease modeling, and fundamental biological research. We also propose the low-hanging fruits along the journey. Creating and growing a virtual yeast cell might be a valid option. As we stand on the brink of this exciting frontier, the collaborative efforts of the scientific community will be crucial in realizing the full potential of AIVC and driving the future of in silico life sciences.
References
Slepchenko, B. M., Schaff, J. C., Macara, I. & Loew, L. M. Trends Cell Biol. 13, 570–576 (2003).
Karr, J. R. et al. Cell 150, 389–401 (2012).
Macklin, D. N. et al. Science 369, eaav3751 (2020).
Ye, C. et al. Biotechnol. Bioeng. 117, 1562–1574 (2020).
Osterlund, T., Nookaew, I., Bordel, S. & Nielsen, J. BMC Syst. Biol. 7, 36 (2013).
Bunne, C. et al. Cell 187, 7045–7063 (2024).
Wang, S. et al. Nat. Methods 21, 2128–2134 (2024).
Dong, Z. et al. Nat. Commun. 15, 9378 (2024).
Qian, L. et al. Cell Genomics 4, 100691 (2024).
Sun, R. et al. bioRxiv A perturbation proteomics-based foundation model for virtual cell construction https://doi.org/10.1101/2025.02.07.637070 (2025).
Sjostedt, E. et al. Science 367, eaay5947 (2020).
Guo, T., Steen, J. A. & Mann, M. Nature 638, 901–911 (2025).
Nordmann, T. M., Mund, A. & Mann, M. Nat. Methods 21, 2220–2222 (2024).
Li, W. et al. Anal. Chem. 97, 1190–1198 (2025).
Dai, T. et al. Nature 635, 890–897 (2024).
EXAMPLE: The Weight of a Cell
A single yeast cell weighs about one million times less than a grain of sand. But how do we know this?
NIKO MCCARTY AUG 18, 2025
Microbes are so small that tens of thousands could fit in the space of the period at the end of this sentence. And yet, for two of the most widely studied kinds — S. cerevisiaeand E. coli — we know their weight with remarkable precision: A single yeast cell weighs about 100 picograms and a single E. coli bacterium weighs about one picogram, or 60 million times less than a grain of sand.
At first blush, measuring the weight of a single cell seems an impossible task. How can we make such a precise measurement with reasonable certainty? A typical kitchen scale has a sensitivity of 0.1 grams, meaning it can detect the difference between a banana weighing 175 grams and another weighing 175.1 grams. By contrast, an E. colicell weighs 100 billion times less than 0.1 grams.
Today, such measurements are made using profoundly clever contraptions developed by scientists over the last couple of decades. These devices can measure individual cells with femtogram precision (a unit 1,000-times smaller than a picogram). But before such precision instruments, scientists had to make do with whatever was already in the lab.
Back in 1953, for example, two biologists from Southern Illinois University (supported, in part, with funding from the Anheuser-Busch brewery)1 invented one of the first methods to determine the weight of an individual yeast cell. And they did it, incredibly, using little more than a microscope, sugar water, and a camera.
Their method made use of Stokes’ law, which describes how a small sphere sinks through a liquid. If the sphere falls without causing turbulence, the liquid “pushes back” with a drag force. In 1845, Sir George Stokes — an Irish mathematician and the longest-serving Lucasian Professor of Mathematics at the University of Cambridge — showed that this drag force is proportional to the sphere’s size, the liquid’s viscosity, and the sphere’s velocity through the fluid. Written as a formula, where r is the sphere’s radius, η is the fluid’s viscosity, and v is the velocity at which the sphere sinks:
Now, this is just the equation for drag force, or the amount of resistance that the fluid exerts on the sphere. But the sphere is also acted on by gravity, which pulls it down, and by buoyancy, which pushes it up! The downward pull is given by the sphere’s weight minus the buoyant force:
Here, d1 is the sphere’s density, d0 is the fluid’s density, and g is gravity. At terminal velocity — meaning, when the sphere falls through the liquid at a steady speed — the downward net force is exactly balanced by the upward drag force. So we can set the two equations against one another to arrive at a final equation:
The brilliance of this equation is that it enables us to figure out the mass of the sphere. All we need to measure is the sphere’s radius, its velocity through the fluid, and the viscosity and density of that fluid. Once those values are known, we plug them into the equation to calculate the sphere’s density. Finally, we multiply this density by the sphere’s volume (determined from its radius) to arrive at a mass.
And that’s exactly what the Southern Illinois researchers did, back in 1953, to figure out the mass of individual yeast cells.
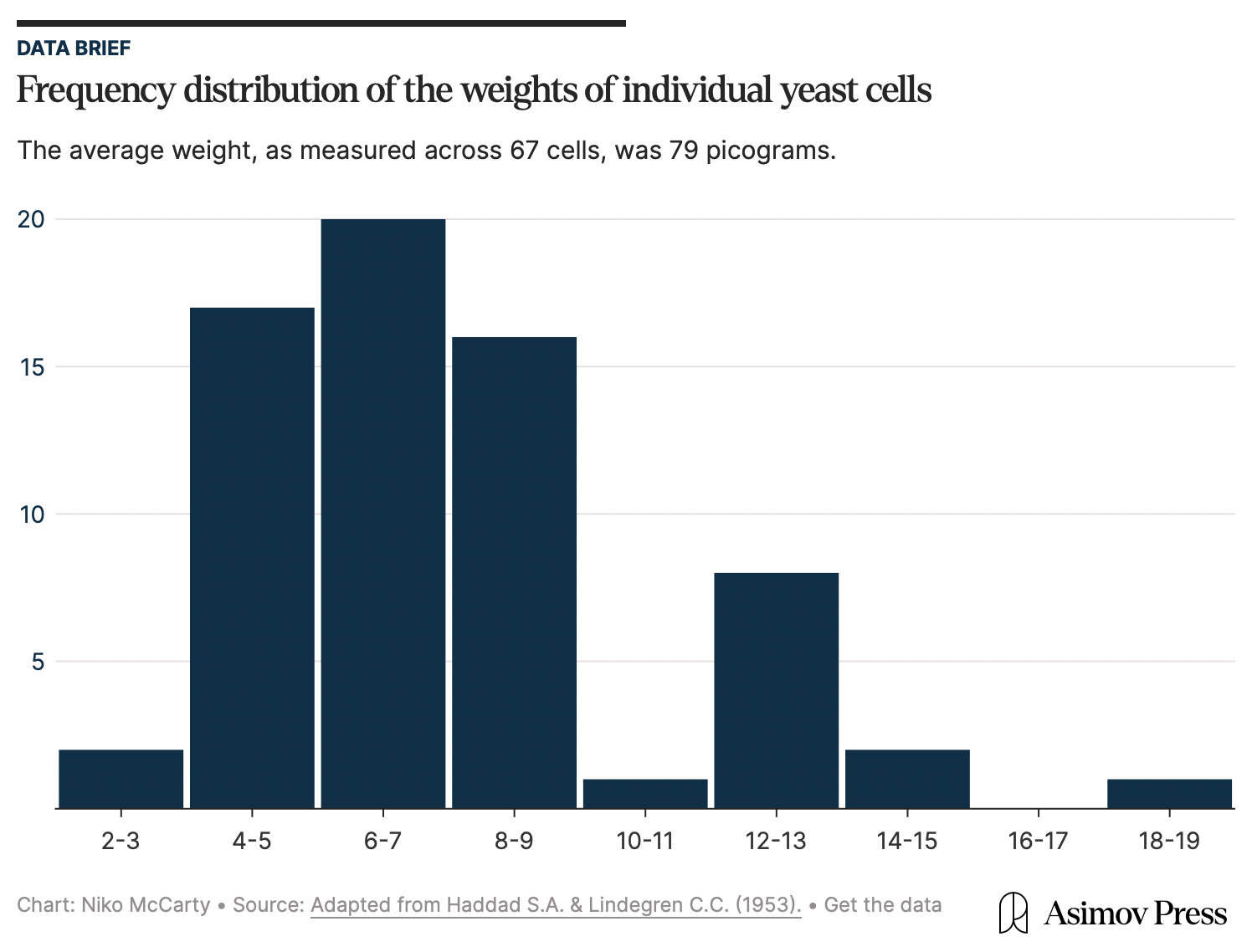
The researchers suspended the cells in a one percent sugar water solution, placed the samples onto a microscope slide, and then propped the slide up vertically. Next, they used a microscope and camera to film time-lapse videos of the yeast cells falling, frame by frame. They did this for 67 of these cells at 400x magnification.
From the photos, the researchers could measure the distance each cell traveled over a fixed time, determining the radius of each using a scale bar. And then — because they already knew the fluid’s viscosity and density — they were able to use Stokes’ law to calculate the weight of an individual cell: 79 picograms, on average: a value remarkably close to estimates made as recently as 2022.

The researchers proceeded as if each yeast cell were spherical — an important assumption because Stokes’ law works only for spheres moving through a fluid. The symmetry of a sphere is what enables an exact calculation of the drag force. And yeast cells, being nearly spherical in real life, mapped onto the assumption well enough for the math to hold.
But not all cells are spheres. E. coli cells, for example, look more like elongated rods. If you were to perform the 1953 experiment on them, the cells would create turbulence, throwing off Stokes’ equations. Measuring a cell like this, therefore, requires a completely different strategy.
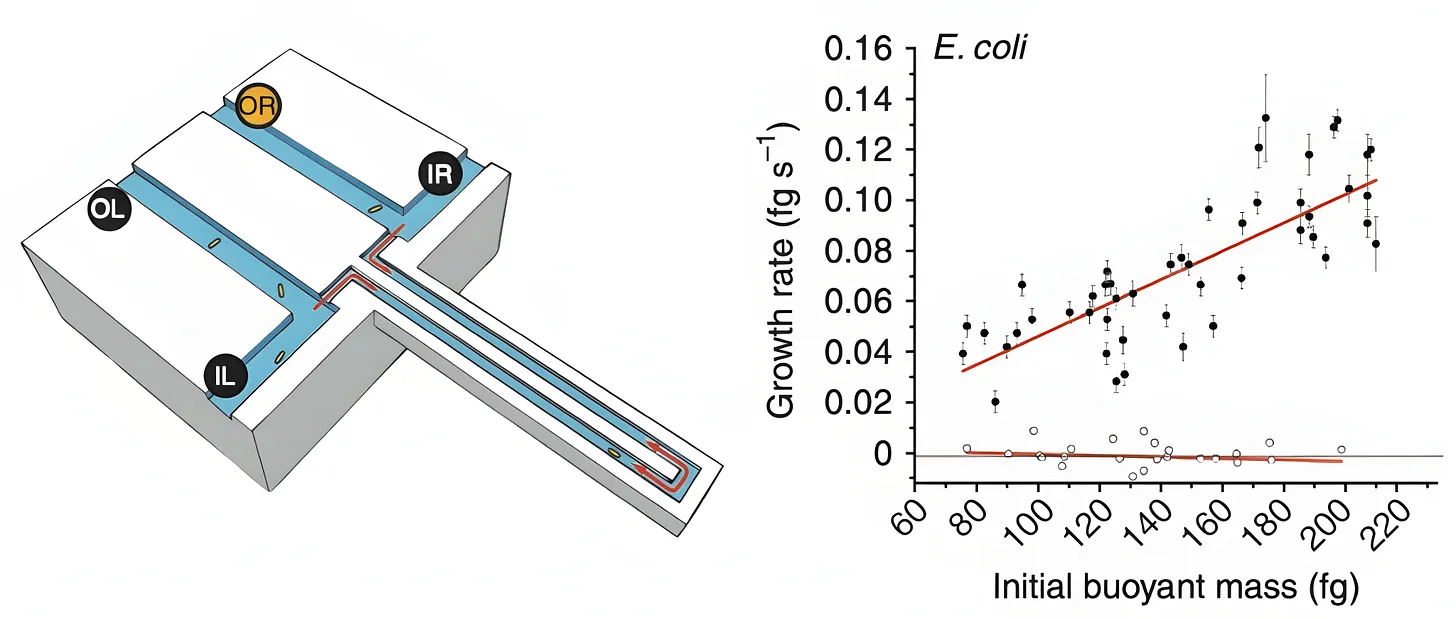
In 2010, MIT scientists came up with a tool for measuring the mass of any single bacterial cell, including E. coli. The device, called “a suspended microchannel resonator,” is basically a “hollow microcantilever beam containing an embedded fluidic microchannel.” The beam has a U-shaped tunnel running through its interior and vibrates very quickly, similar to a guitar string.
As a single cell floats through the channel in this beam, the beam’s vibration changes ever so slightly. Heavier cells shift the frequency more. Those frequency shifts are what allow researchers to figure out the cell’s “buoyant mass,” or how much heavier the cell is compared to water.2 Such measurements have femtogram precision, meaning they can detect changes between two masses 1,000-times smaller than a bacterium’s weight.
The device can also be used to measure the same cell again and again, meaning researchers can track the growth of the cell over time. After a cell passes through the vibrating beam and its mass is recorded, researchers reverse the flow of liquid and send it back through the channel in the opposite direction. If the procedure is repeated quickly and often enough, the cell becomes trapped at the end of the vibrating beam. Each pass yields a new frequency measurement and, as the cell grows, the frequency shift increases proportionally to its added mass.
When the authors measured 48 individual cells and averaged the results, they found that a typical E. coli weighs about 0.55 picograms. But this number is constantly in flux because the growth rate increases in proportion to cell size. At 37 °C, the smallest cells added about 0.06 picograms of mass per hour, while the largest gained closer to 0.14 picograms per hour.
The beauty of these experiments is how they bring basic mathematics to bear on biology. The yeast experiment, in particular, evokes the famous 19th-century work by Lord Rayleigh, in which he calculated the size of a single molecule using only oil and water.
In 1890, Rayleigh realized that the thickness of a molecular film could be found by dividing its volume by the area it covered. In his at-home laboratory, Rayleigh placed a small droplet of oil onto a calm water surface and watched the oil spread into an impossibly thin sheet. By measuring the surface area that the drop covered, he calculated the film’s thickness as 1.6 × 10−7 centimeters, and correctly deduced this to be the length of a single oil molecule. Impressively, Rayleigh’s estimate was off by just 18.5 percent when benchmarked against modern measurements of those same molecules, made using X-rays and sophisticated equipment.
All of these experiments share the same quality: They take a phenomenon that seems difficult to measure and overcome this difficulty through mathematics and first principles thinking. Such experiments are timeless; a reminder that we don’t have to overcomplicate either our tools or our questions to make immense contributions to biology. Cells are physical objects — collections of molecules with real weights, shapes, and speeds. Think of them as such, and anything can be measured.
Niko McCarty is a founding editor of Asimov Press.
Cite: McCarty, N. “The Weight of a Cell.” Asimov Press (2025). https://doi.org/10.62211/51hg-87ty
Breweries have been patrons of yeast science for more than a century. In 1876, the Carlsberg Laboratory in Copenhagen became one of the first industrial labs devoted entirely to brewing research, leading to the isolation of Saccharomyces pastorianus, the species used to make lager beer.
The beam is first calibrated using polystyrene beads of a known size and density. A laser sensor measures the beam’s vibrations, which, based on the calibration measurements, help determine the mass of individual cells.


